
from the - Wind Powered Generators - "Nice to Know" series
at reasonablepower.com
(quoted from reasonablepower.com . The best place to get your wind energy conversion system.)

Generally we start with a question, such as:
What is the wind load on a flat plate which is round and has a diameter of 14 ft. and which has a 50 mile per hour wind hitting it?
ANSWER:
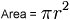
Area = A = (3.14159)(7 ft)(7 ft) = 153.93791 square feet
or in SI units; Area = 14.30129981 square meter
Wind Speed = v = 50 mph
or in SI units; Wind Speed = 22.352 meter/second
Using the formula:
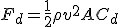
where
Fd is the force of drag (or in this case Force Against the flat plate),
p is the density of the air,
v is the speed of the air against the object,
A is the area of the object which the air is blowing against,
Cd is the drag coefficient,
The density of air at sea level is about 1.2 kg/m^3 (1.2 kilo grams per cubic meter) .
p = 1.2 kilogram/cubic meter (for this example)
The drag coefficient for a flat plate in open air is about 1.28
Cd (which is a dimensionless constant)= 1.28 (for this example)
Thus:
Fd = (1/2)(1.2 kilograms/cubic meter)(22.352 meter/second)(22.352 meter/second)(14.30129981 square meter)(1.28)
Fd = 5487.4351 kilogram meter / second^2 = 5487.4351 Newton
Fd = 39690.69 pound foot/second^2
or
F = 39,690.69 pounds
If (for example) we are working with a wind powered generator which has 4' long blades, and each blade starts at 3' from the center, we want to subtract the Fd of a 6' diameter flat plate from the Fd of the 14' flat plate.
First we substitute the areas:
Area = A = (3.14159)(3 ft)(3 ft) = 28.27431 square feet
or in SI units; Area = 2.626769353 square meters
Fd = (1/2)(1.2 kilograms/cubic meter)(22.352 meter/second)(22.352 meter/second)(2.626769353 square meter)(1.28)
Fd = 1007.896502 kilogram meter / second^2 = 1007.896502 Newton
Fd = 7290.129364 pound foot / second^2
or
F = 7,290.129364 pounds
Then we subtract the two forces:
39,690.69 pounds - 7,290.129 pounds = 32,400.561 pounds [or pounds force] [or pound foot / square second]
We can use this in both calculating the wind load and in calculating the center shaft torque for horsepower.
If (for example) we are working with a wind powered generator which has it's blades (currently) set at a 45 degree angle, then (in an ideal theoretical situation) we could use the hypotenuse formula and a little bit of trigonometry for right triangles to calculate the lift and drag. The force of the wind as drag against the blades forcing them back would be (the wind load at 90 degrees, which is the hypotenuse) multiplied by (the sine of 45 degrees) = (32,400.561 pounds)x(0.70711) = 22,910.760 pounds. Since the blades are set at a 45 degree angle, the force turning the blades is the same amount as the force of drag against the blades. Notice that the (ideal theoretical) wind load against the blades is now 22,910.760 pounds instead of 32,400.561 pounds because the blades are on an angle.
If we want to verify this, we multiply the squares of the lift and drag at 45 degrees, take the square root of that, and then check that against the wind load at 90 degrees.
(22,910 pounds)(22,910 pounds) + (22,910 pounds)(22,910 pounds) = (524,868,100) + (524,868,100) = 1,049,736,200
Square root of 1,049,736,200 = 32399.627 , or rounded up it is 32,400
We rounded our numbers as we went along in this example, so close is fine.
Thus:
We have about 22,910 pounds turning the blades.
And, we have about 22,910 pounds of wind load.
If (for example) we are working with a wind powered generator which has it's blades centered at 100' above the ground, to get the cantilever torque (of the blades, and only the blades) which is attempting to bend the support at it's base, we multiply the wind load against the height.
That, in this case, is the wind load of the blades (set at a 45 degree angle), and it does not include the support, nor any of the structure.
Cantilever Torque (by the blades alone) attempting to bend the support at it's base = Tc = Force x distance = (22,910.76 pounds) x (100')
Tc = 2,291,076. foot pounds.
If (for example) we want to know how much torque this generates against the shaft, we spread out the force per area of the blades and per distance from the center of the shaft and calculate that.
That is another topic. Remember that at this point we have not included occasional wind shear, nor resistance of the bearings, etc.
Reference:
NASA: drag coefficient.
Kind of nice, using wind for energy.
Brought to you by a supporter of http://www.reasonablepower.com